Research Focus

The goal of our group is to advance computational design technologies (with a particular emphasis on topology optimization methods) to produce superior structural designs that are manufacturable and economical, while pushing the limits of structural efficiency. Our research spans:

• multiple scales, from architected materials design to structural assemblies;
• single and multi-material designs, including multiple isotropic or anisotropic (e.g., composite) materials
• different manufacturing processes, including additive manufacturing, composites manufacturing, welding and casting; and
• multiple application realms and physics.

The following are some areas of ongoing work.

Ongoing Research Work

Design of structural assemblies Topology optimization has often been used for the design of single structural components. Prevalent methods represent the design using fields, thus rendering highly efficient, organic designs. These designs, however, do not conform to structures that are to be produced as the assembly of geometric primitives (e.g., stock material). Over the last years, our group has been advancing techniques (collectively known as the geometry projection method) to perform the topology optimization of structures that are made by  the combination of geometric primitives.
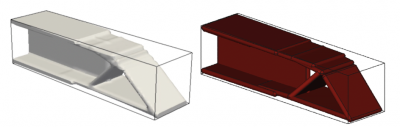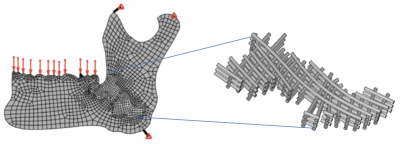
Topology optimization of architected materials One area where geometry projection techniques fit naturally is in the design of architected truss lattice materials to obtain desired properties. While truss lattices underperform thin-wall periodic materials in terms of stiffness-to-weight ratio, their open-cell configuration allows for their fabrication via additive manufacturing techniques. Over the last years, we have advanced topology optimization techniques to design truss lattice materials. Our techniques simultaneously determine the spatial layout of the struts within the unit cell and a) the best choice of material for each strut out of a set of available materials or b) the fraction of hole (for tubular struts) or fiber reinforcement (for struts made of a composite).
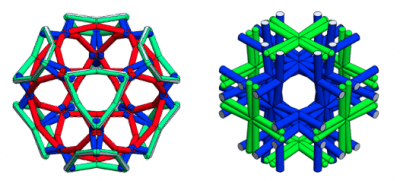Design of structural assemblies made with composite materials Another focus of our work is in advancing topology optimization techniques to design structural assemblies made of fiber-reinforced primitives (e.g., bars and plates). Our methods simultaneously determine the optimal layout of the primitives within a 3-dimensional design region and the fiber reinforcement of each primitive. The goal of these methods is to render designs that are amenable to conventional composite manufacturing processes for, e.g., structures made of laminates.
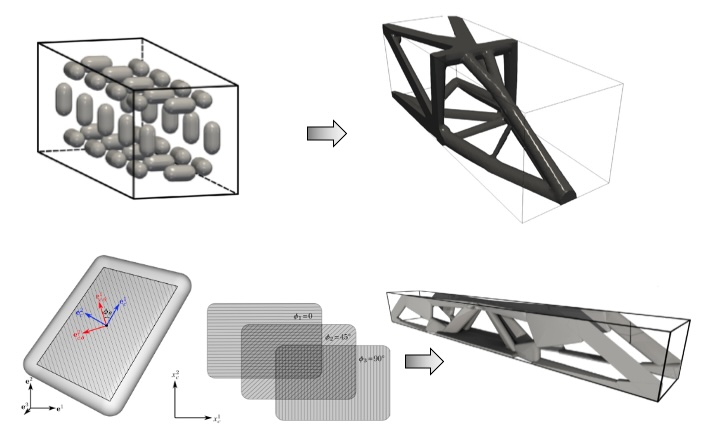Design for manufacturability An important consideration in the design of structural assemblies and components is to ensure the design can be easily and economically manufactured. In addition to designing assemblies made of stock material, we have advanced topology optimization techniques to minimize manufacturing cost subject to structural performance criteria, and to produce designs that are made of multiple types of components that are amorphous at the initial design and subsequently differentiate into CAD-friendly primitives in the optimization.
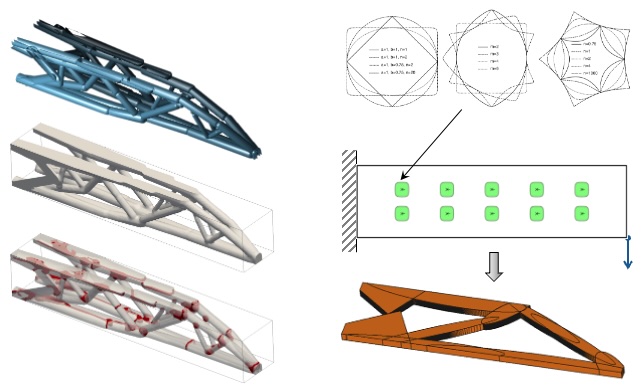Design of synthetic bone scaffolds Another significant area of interest is the computational design of synthetic bone scaffolds fabricated by additive manufacturing (direct ink writing) to repair bone defects. As with all of our research efforts, an important goal is to render designs that conform to the manufacturing process. We have advanced techniques to design scaffolds based on purely mechanical criteria (e.g., stiffness) and more recently on bone growth criteria, whereby bone growth into the scaffold is simulated using a time-dependent model in which the bone deposition rate is a function of a mechanical stimulus and the concentration of growth cells.
Incorporation of local failure criteria in topology optimization Our group has also made strides in incorporating into the optimization local failure criteria, such as stress and fatigue life constraints. We have formulated techniques to efficiently impose maximum stress and minimum (high-cycle) fatigue life for large-scale problems. In particular, the incorporation of fatigue life constraints considers non-proportional loading, which is common in many practical applications. Recently, we advanced a method to impose stress constraints that does not require adaptive constraint scaling (ACS) to tightly enforce the stress constraint, and that exhibits better convergence and designs than the ACS approach.
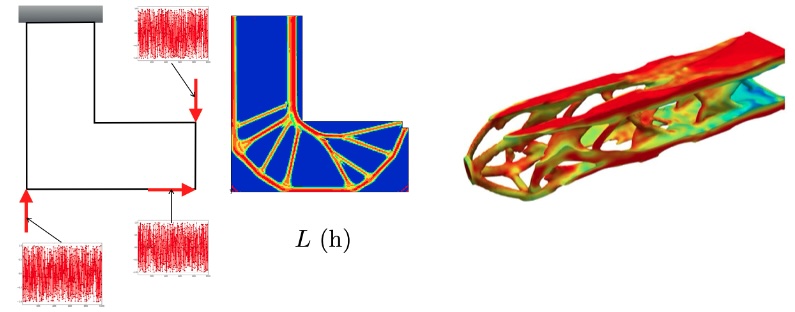Topology optimization for energy applications A recent focus of our work is to advance topology optimization techniques to design efficient energy systems. An ongoing effort is to employ geometry projection methods to design the flow structures in a plate heat exchanger to maximize the heat transfer performance while ensuring an acceptable pressure drop.
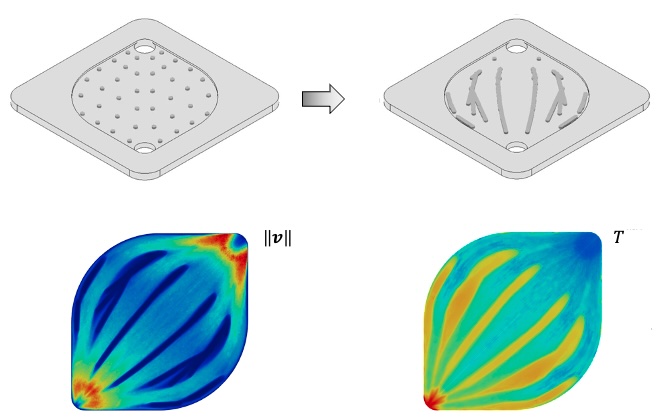